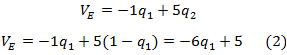La teoría de juegos es un área que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados juegos) y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. La teoría de juegos se formalizó por primera vez con a parir de los trabajos de John Von Neumann y Oscar Mongenstern antes y durante la Guerra Fría, debido a su aplicación en la estrategia militar.
En pocas palabras la teoría de juegos estudia la elección de la conducta óptima cuando los costes y los beneficios de cada opción no están determinados de antemano sino que dependen de las elecciones de otros individuos.
Los juegos estudiados por la teoría de juegos están bien definidos por objetos matemáticos. Un juego consiste en un conjunto de jugadores, un conjunto de movimientos (o estrategias) disponible para esos jugadores y una especificación de recompensas para cada combinación de estrategias. La representación de un juego se hace mediante una matriz, llamada matriz de pagos, donde se relacionan las estrategias de cada jugador y las recompensas en cada combinación, por ejemplo, consideremos el juego piedra, papel o tijera, donde el perdedor debe pagar una unidad monetaria al ganador y en caso de empate no hay pago para ninguno. La siguiente tabla puede considerarse una matriz de pagos para el juego:
Piedra | Papel | Tijera | |
Piedra | 0 | -1 | +1 |
Papel | +1 | 0 | -1 |
Tijera | -1 | +1 | 0 |
En esta matriz los números negativos son las ganacias del jugador fila, mientras que los números positivos son las ganancias del jugador columna.
Estrategias y tipos de estrategias
En teoría de juegos, la estrategia de un jugador es un plan de acción completo para cualquier situación que pueda ocurrir; determina completamente la conducta del jugador. La estrategia de un jugador determinará la acción que tomará el jugador en cualquier momento del juego, para cualquier secuencia de acontecimientos hasta ese punto.
El concepto de estrategia se confunde (erróneamente) en ocasiones con el de movimiento. Un movimiento es una acción que toma un jugador en un determinado momento en el juego . Una estrategia, por otra parte, es un algoritmo completo para jugar al juego, enumerando implícitamente todos los movimientos de todos los jugadores para cada situación del juego.
Las estrategias pueden ser de dos tipos: puras o aleatorizadas.
Estrategia pura.
Una estrategia pura proporciona una definición completa para la forma en que un jugador puede jugar a un juego. En particular, define, para cada elección posible, la opción que toma el jugador. El espacio de estrategia de un jugador es el conjunto de estrategias puras disponible al jugador.
Estrategia aleatorizada.
Una estrategia mezclada es una asignación de probabilidad a cada estrategia pura. Define una probabilidad sobre las estrategias y refleja que, en lugar de elegir una estrategia pura particular, el jugador elegirá al azar una estrategia pura en función de la distribución dada por la estrategia mezclada. Por supuesto, cada estrategia pura es una estrategia mezclada que elige esa estrategia pura con probabilidad p y cualquier otra con probabilidad q.
Juegos estrictamente determinados
Un juego estrictamente es aquel en cual se le puede determinar directamnete su solución es decir, su valor de juego. Para determinar la solución de un juego que está estrictamente determinado se busca reducirlo por predominio y/o utilizar el criterio minimax.
Cuando analizamos cualquier juego, hacemos los siguientes supuestos acerca de los dos jugadores:
Un jugador quien usa el criterio minimax escoge una estrategia que, entre todas las estrategias posibles, minimiza el daño de la mejor contra-estrategia del otro jugador. Es decir, una estrategia óptima según el criterio minimax es una que minimiza el daño máximo que puede hacer el contrincante. Para ilustrar esto, vamos a ver el siguiente ejemplo:
Juegos estrictamente determinados
Un juego estrictamente es aquel en cual se le puede determinar directamnete su solución es decir, su valor de juego. Para determinar la solución de un juego que está estrictamente determinado se busca reducirlo por predominio y/o utilizar el criterio minimax.
Cuando analizamos cualquier juego, hacemos los siguientes supuestos acerca de los dos jugadores:
- Cada jugador hace la acción mejor posible.
- Cada jugador sabe que su contrincante está también haciendo la acción mejor posible.
Un jugador quien usa el criterio minimax escoge una estrategia que, entre todas las estrategias posibles, minimiza el daño de la mejor contra-estrategia del otro jugador. Es decir, una estrategia óptima según el criterio minimax es una que minimiza el daño máximo que puede hacer el contrincante. Para ilustrar esto, vamos a ver el siguiente ejemplo:
Observamos que en la matriz de pagos tanto el jugador fila como el jugador columna tienen tres posibles estrategias, además vale la pena aclarar que los valores negativos son ganancia para el jugador columna y lo s positivos ganancias para el jugador fila; ahora, aplicando el criterio minimax, tenemos que para el jugador fila lo peor que le puede ocurrir en cada estrategia es lo siguiente:
Estrategia I: -3 (perder 3)
Estrategia II: -2 (perder 2)
Estrategia III: 4 (ganar 4)
haciendo lo mismo para el jugador columna, tenemos:
Estrategia I: 6 (perder 6)
Estrategia II: 5 (perder 5)
Estrategia III: 4 (perder 4)
El juego tendrá solución inmediata si un valor se encuentra tanto en lo peor para el jugador fila como para el jugador columna, a este valor se le llama punto de silla. En el ejemplo el punto de silla es 4, que resulta de aplicar la estrategia III por ambos jugadores. Esto sólo ocurre cuando el juego está estrictamente determinado.
Dominancia de estrategias
Una acción domina a otra si todos sus pagos son por lo menos tan provechoso al jugador que los pagos correspondientes de la otra. En términos de la matriz de pagos, podemos decirlo como sigue: - a) Renglón r en la matriz de pagos domina a renglón s si cada pago en renglón r ≥ el pago correspondiente en renglón s.
- b) Columna r en la matriz de pagos domina a columna s si cada pago en columna r ≤ el pago correspondiente en columna s.
Si dos renglones o columnas son iguales, cada uno domina al otro. Un renglón o columna domina estrictamente a un otro si el uno domina al otro y son desiguales.
Siguiendo el primero principios de la teoría de juegos, la acción que corresponde a un renglón o columna estrictamente dominado nunca será jugado, y ambos jugadores son conscientes de esto por el segundo principio. Entonces cada jugador quien sigue los principios de la teoría de juegos eliminará repetidamente renglones y columnas dominadas como podría ser el caso. En el caso que son iguales dos renglones o columnas, no hay razón para elegir uno sobre el otro, entonces cualquiera de los dos puede ser eliminado. Este proceso se llama reducción por predominio. Ejemplo:
Dada el siguiente juego, obtener el valor del juego, reduciendo renglones y columnas, mediante la predominancia.
Los pagos del renglón 2 son todos mayores a los pagos del renglón 1, entonces el renglón 2 domina al renglón 1. Eliminando el renglón 1 queda lo siguiente:
Observamos que la columna B domina a las columnas A y C, por lo tanto podemos eliminar ambas columnas dominadas.
Por últimmo, el renglón 1 domina al renglón 2:
Por lo tanto el jugador renglón debe jugar la estrategia II y el jugador columna, la estrategia B. El valor del juego es 0, es decir es un juego justo.
Juegos con estrategias aleatorizadas
Pero tenemos que:
Pero tenemos que:
Juegos con estrategias aleatorizadas
Cuando un juego no está estrictamente determinado, para hallar su solución se debe hacer asignar probabilidades a cada estrategia, es decir crear estrategias aleatorizadas. Para resolver un juego cons estrategias aleatorizadas, se hace uso de dos métodos: el gráfico, que se aplica solo a juegos que involucran matrices de pagos 2x2, es decir que tienen hasta dos estrategias por jugador, y el método simplex que se aplica de manera general a todos los juegos.
A continuación vamos a ver un ejemplo de la resolución de un juego por medio del método gráfico.
Supongamos que tenenmos el siguiente juego:
Este juego no está estrictamente determinado, por lo tanto debemos asignarle probabilidades a cada una de las alternativas por jugador.
para saber que probabilidades tenemos que asignarle a cada alternativa, se procede de manera seprada para cada jugador, asi:
Para el jugador renglón:
p1: la probabilidad de elegir la estrategia I
p2: la probabilidad de elegir la estrategia II.
p1 + p2 = 1
Ahora tenemos que hallar las ecuaciones que resultan al determinar los valores esperados por el jugardor renglón, teniendo en cuenta lo que juega el jugador columna.
Si el jugador columna elige la estrategia I, el valor esperado por en jugador renglón es:
Entonces nos queda:
Si el jugador columna juega la estrategia II:
Ahora se procede a graficar las dos ecuaciones:
Para la ecuación 1:
Si p1 = 0, entonces Ve = -1
Si p1 = 1, entonces Ve = 3
Para la ecuación 2:
Si p1 = 0, entonces Ve = 5
Si p1 = 1, entonces Ve = -2
La gráfica queda de la siguiente manera:
La p1 que garantiza la mejor situación para el jugador renglón, independientemente lo que juegue el jugador columna, es el punto donde se cruzan las dos rectas. Para saber exactamente cual es ese punto, basta con igualar ambas ecuaciones y despejar p1.
Ahora reemplazando el valor de p1 en la ecuación 1, obtenemos el valor esperado:
El valor de p2 será:
Para el jugador columna se procede de la misma manera.
q1= probabilidad de escoger la estrategia 1
q2= probabilidad de escoger la estrategia 2.
Si el jugador renglón elige la estrategia I, el valor esperado por en jugador renglón es:
Entonces nos queda:
Si el jugador renglón juega la estrategia II:
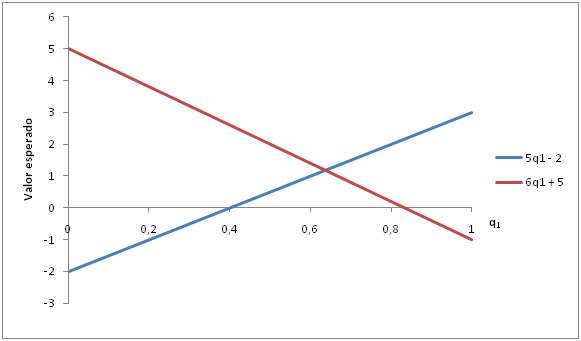
Ahora se procede a graficar las dos ecuaciones:
Para la ecuación 1:
Si q1 = 0, entonces Ve = -2
Si q1 = 1, entonces Ve = 3
Para la ecuación 2:
Si q1 = 0, entonces Ve = 5
Si q1 = 1, entonces Ve = -1
Hallamos el punto de corte:
Reemplazamos q1 en la ecuación 1:
Para hallar q2:
Obsérvese que le valor del juego es igual para el jugador renglón que para el jugador columna, por lo que podemos afirmar que el juego es justo.